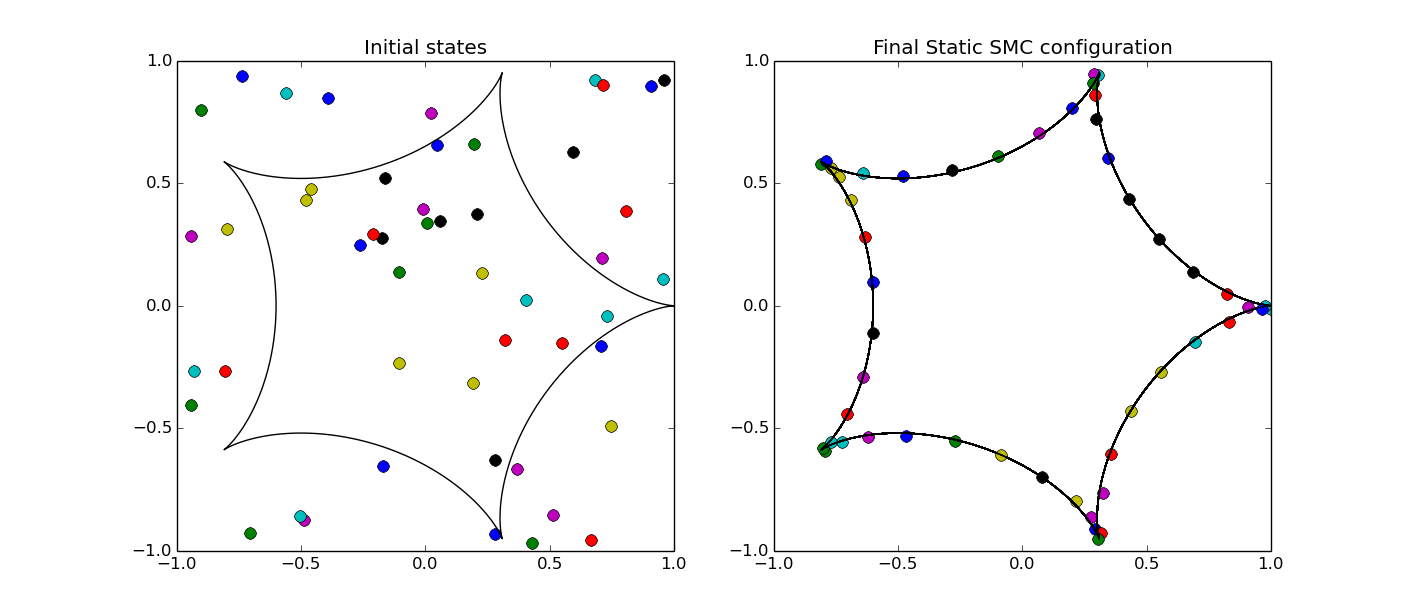
Coverage of curves

Yes, you can cover curves also with the SMC approach. Here is an example.

# First define a function correponding to a parametric curve
def hypocycloid_curve(theta, r=0.2, k=5):
    """ defines parametric curve for hypocycloid curve """
    x = r * (k-1) * cos(theta) + r * cos((k-1) * theta)
    y = r * (k-1) * sin(theta) - r * sin((k-1) * theta)
    return x, y

# After necessary imports
# Define probability distribution
prob_dist = ProbDist(xmin=-1.0, xmax=1.0, ymin=-1.0, ymax=1.0)

# set probability distribution on curve
prob_dist.set_prob_dist_on_curve(hypocycloid_curve, np.arange(0, 2*pi, 0.01))

# Define StaticSMC coverage object
static_smc = StaticSMC(prob_dist)

# Add agents (with random initial locations) to coverage object
for _ in range(50):
    static_smc.add_agent(Agent(random.random(), random.random()))

# Run the algorithm (100 time-steps of size 0.01)
static_smc.time_steps(100, 0.01) 

Below is shown the initial random locations of the agents and the final optimal configuration obtained using Static SMC. The black curve is the hypocyloid curve that needs to be covered. To see the full code for this example, look here.