Introduction

SMC provides a suite of algorithms meant to solve various coverage problems using multi-agent systems. SMC is a simple yet effective approach for solving such coverage problems. The algorithms in this library are primarily based on ideas presented in these two papers:

1. A Static Coverage Algorithm for Locational Optimization
2. Metrics for ergodicity and design of ergodic dynamics for multi-agent systems

Download and Install

To download the smc repository simply do:

git clone https://github.com/qpcode/smc.git

To install the smc package, go into the smc repo directory and simply do:

python setup.py install

Use sudo based on whether you want to install the package as a superuser. Also, in case your machine doesn’t satisfy the requirements, create a virtualenv, activate it and then install the smc requirements by going into the smc repo directory and doing:

pip install -r requirements.txt

Static Coverage problems

The first kind of coverage problem is where one is interested finding a static configuration of agents that is optimized for coverage of a probability distribution. For example, if one wants to place 9 agents that optimally cover a uniform distribution on a square domain, here is how one can do it with Static SMC.

# After necessary imports
# Define probability distribution and StaticSMC object
prob_dist = ProbDist(xmin=0.0, xmax=1.0, ymin=0.0, ymax=1.0)
static_smc = StaticSMC(prob_dist)

# Add agents (with random initial locations) to coverage object
for iagent in range(9):
    static_smc.add_agent(Agent(random.random(), random.random()))

# Run the algorithm (2000 time-steps of size 0.01)
static_smc.time_steps(2000, 0.01) 

Below is shown the random initial locations of the agents together with the final optimal configuration obtained using Static SMC. As can be seen, the agents get naturally arranged in an approximate 3 X 3 grid. To see the full code for this example, look here.

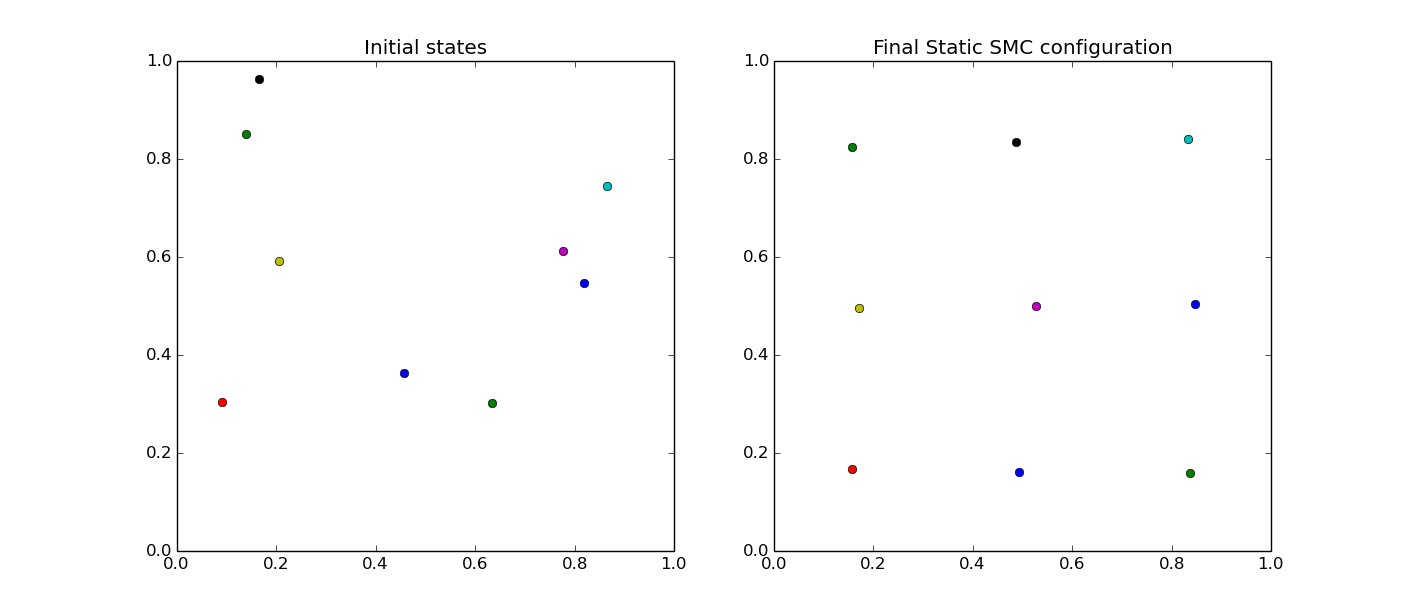
Here is a listing of other static coverage examples:

1. Static Coverage of a Gaussian distribution.
2. Static Coverage of domains with holes.
3. Static Coverage of curves.
4. Generate Pointillism art.

Solving various coverage problems boils down to setting up interesting probability distributions. To see how to set up interesting probability distributions, see the API for the ProbDist class.

Dynamic Coverage problems

These kind of coverage problems arise when one is interested in planning trajectories for agents so that they visit (or come close to visiting) every single point in the domain. For example, if one wants to plan trajectories for four agents so that they explore a square domain uniformly, one can do it with Dynamic SMC as follows:

# After necessary imports
# Define probability distribution and DynamicSMC object
prob_dist = ProbDist(xmin=0.0, xmax=1.0, ymin=0.0, ymax=1.0)
dynamic_smc = DynamicSMC(prob_dist)

# Add agents (with random initial locations) to coverage object
for iagent in range(4):
    dynamic_smc.add_agent(Agent(random.random(), random.random()))

# Run the algorithm (1000 time-steps of size 0.01)
trajectories = dynamic_smc.time_steps(1000, 0.01, return_trajectories=True) 

The left and right figures below shown the trajectories after 500 time-steps and 1000-time-steps respectively. As can be seen, the gaps left between trajectories become smaller as time proceeds. To see the full code for this example, look here.

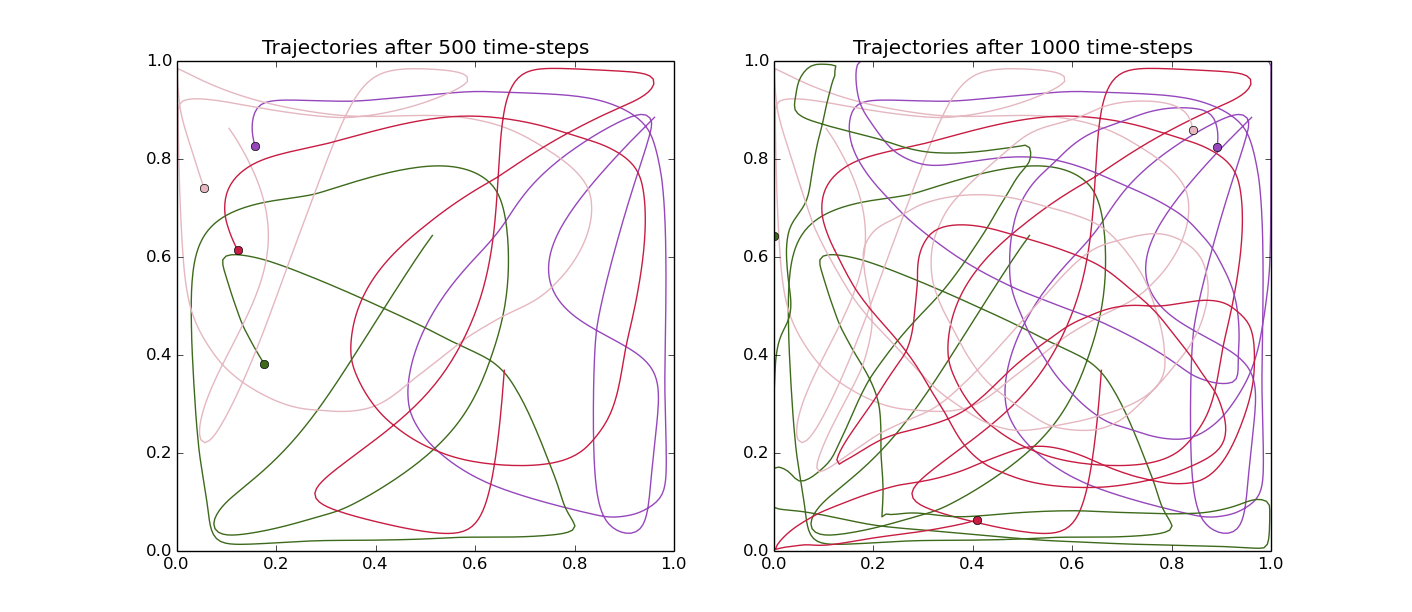
Here is a listing of other dynamic coverage examples:

1. Dynamic Coverage of a bimodal distribution.
2. Dynamic Coverage of a non-convex domain.
3. Dynamic Coverage of a moving target distribution.
4. Generate watercolor-like paintings.

Related Work

Some links to related work are provided below:

1. Ergodic Exploration of Distributed Information.
2. Autonomous Visual Rendering using Physical Motion.
3. Multi-Agent Ergodic Coverage with Obstacle Avoidance.
4. A Julia package for generating ergodic trajectories using projection-based optimization and smc

Contact

For any questions or ideas regarding this library, contact me at ergodicrobots@gmail.com